C3 linearization

C3 linearization演算法可以拿來解決多重繼承的方法優先呼叫順序(Method Resolution Order)。

以下是經典的diamond problem

    A
  /   \
 B     C
  \   /
    D

B繼承A, C繼承A, D繼承B, C。

由於在C++內沒有實作，所以這樣寫是會產生錯誤的。

#include <iostream>

using namespace std;

class A {
    public:
    void foo() {
        cout << "I'm A" << endl;
    }
};

class B: public A {
    public:
    void foo() {
        cout << "I'm B" << endl;
    }
};

class C: public A {
    public:
    void foo() {
        cout << "I'm C" << endl;
    }
};

class D: public B, C {};

int main()
{
    D d = D();
    d.foo();

    return 0;
}

$ clang diamond.cpp
# diamond.cpp:31:7: error: member 'foo' found in multiple base classes of
#       different types
#     d.foo();
#       ^
# diamond.cpp:14:10: note: member found by ambiguous name lookup
#     void foo() {
#          ^
# diamond.cpp:21:10: note: member found by ambiguous name lookup
#     void foo() {
#          ^
# 1 error generated.

但在python3卻有不一樣的結果

class A:
    def foo(self):
        print("I'm A")

class B(A):
    def foo(self):
        print("I'm B")

class C(A):
    def foo(self):
        print("I'm C")

class D(B,C): pass

class E(C,B): pass

d = D()
d.foo() # I'm B

e = E()
e.foo() # I'm C

與c++不一樣就算了，連D, E的結果也不一樣，會早成這樣的原因主要是因為python3有對於這種繼承來繼承去的關係做一層解決方案，他們所採用的就是C3 linearization

L(target) := [target] + merge( L(target_parent1),
                               L(target_parent2),
                               ... ,
                               [target_parent1, target_parent2 ...])

L: C3 linearization的function

merge: 合併C3 linearization結果，而合併的流程如下

第一組開始，抓第一個單位，且不能出現在其他組的非第一個位置(若是其他組的第一個位置則可以)，
- 符合需求，把他從所有的list中抽出來，從頭開始新一輪的尋找
- 不符合需求，遞延找下一組，若遞延到最後一組了，仍沒有符合條件，則停止尋找

從D繼承B, C的例子來看, 應該可以得到下面式子

L(D) := [D] + merge(L(B), L(C), [B, C])

在計算之前我們需要先知道L(B), L(C)的結果，所以先計算L(B), L(C)

L(A) := [A]  // 因為A沒有parent，所以list僅有自己

L(B) := [B] + merge(L(A), [A])
      = [B] + merge([A], [A])
      = [B, A]

L(C) := [C] + merge(L(A), [A])
      = [C] + merge([A], [A])
      = [C, A]

有了以上結果之後我們回到第一個式子

L(D) := [D] + merge(L(B), L(C), [B, C])
L(D) := [D] + merge([B, A], [C, A], [B, C])
L(D) := [D, B] + merge([A], [C, A], [C]) // 先找第一個A，但A出現在第二組的非第一個位置，所以順延找第二組的第一個C，符合需求
L(D) := [D, B, C] + merge([A], [A], [])
L(D) := [D, B, C, A]

有了以上結果之後，我們可以看一下mro到底是不是這樣，可以用以下程式碼驗證

class A:
    def foo(self):
        print("I'm A")

class B(A):
    def foo(self):
        print("I'm B")

class C(A):
    def foo(self):
        print("I'm C")

class D(B,C): pass

class E(C,B): pass

print(D.mro())
# [<class '__main__.D'>, <class '__main__.B'>, <class '__main__.C'>, <class '__main__.A'>, <class 'object'>]

看起來跟預期的結果一樣，(σﾟ∀ﾟ)σ

在wiki介紹那邊有一個比較激烈的例子，這邊直接摘錄實戰一下

情境如下

繼承圖

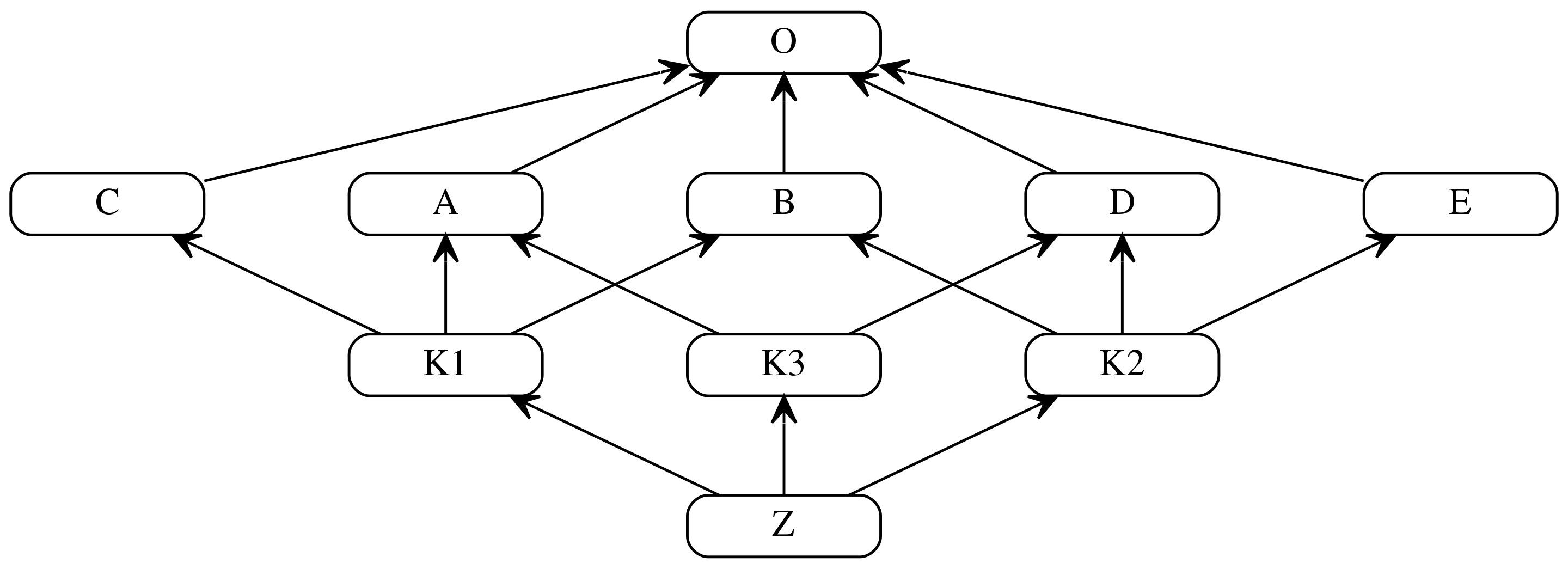
class O
class A extends O
class B extends O
class C extends O
class D extends O
class E extends O
class K1 extends A, B, C
class K2 extends D, B, E
class K3 extends D, A
class Z extends K1, K2, K3

則

L(O) := [O]  // O沒有parent了，只有一個O

L(A) := [A] + merge(L(O), [O])
      = [A] + merge([O], [O])
      = [A, O]

// 下面幾個同L(A)，就不寫出推演過程了
L(B)  := [B, O]
L(C)  := [C, O]
L(D)  := [D, O]
L(E)  := [E, O]

L(K1) := [K1] + merge(L(A), L(B), L(C), [A, B, C])
       = [K1] + merge([A, O], [B, O], [C, O], [A, B, C])
       = [K1, A] + merge([O], [B, O], [C, O], [B, C]) // 從第一組第一個的O開始找，但是O有出現在第二組的尾巴和第三組的尾巴，順延第二組的B，符合條件
       = [K1, A, B] + merge([O], [O], [C, O], [C])
       = [K1, A, B, C] + merge([O], [O], [O])
       = [K1, A, B, C, O]

L(K2) := [K2] + merge(L(D), L(B), L(E), [D, B, E])
       = [K2] + merge([D, O], [B, O], [E, O], [D, B, E])
       = [K2, D] + merge([O], [B, O], [E, O], [B, E])
       = [K2, D, B] + merge([O], [O], [E, O], [E])
       = [K2, D, B, E] + merge([O], [O], [O])
       = [K2, D, B, E, O]

L(K3) := [K3] + merge(L(D), L(A), [D, A])
       = [K3] + merge([D, O], [A, O], [D, A])
       = [K3, D] + merge([O], [A, O], [A])
       = [K3, D, A] + merge([O], [O])
       = [K3, D, A, O]

L(Z)  := [Z] + merge(L(K1), L(K2), L(K3), [K1, K2, K3])
       = [Z] + merge([K1, A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K1, K2, K3])
       = [Z, K1] + merge([A, B, C, O], [K2, D, B, E, O], [K3, D, A, O], [K2, K3])        // A失敗，找K2
       = [Z, K1, K2] + merge([A, B, C, O], [D, B, E, O], [K3, D, A, O], [K3])            // A失敗，D失敗，找K3
       = [Z, K1, K2, K3] + merge([A, B, C, O], [D, B, E, O], [D, A, O])                  // A失敗，找D
       = [Z, K1, K2, K3, D] + merge([A, B, C, O], [B, E, O], [A, O])
       = [Z, K1, K2, K3, D, A] + merge([B, C, O], [B, E, O], [O])
       = [Z, K1, K2, K3, D, A, B] + merge([C, O], [E, O], [O])
       = [Z, K1, K2, K3, D, A, B, C] + merge([O], [E, O], [O])                           // O失敗，找E
       = [Z, K1, K2, K3, D, A, B, C, E] + merge([O], [O], [O])
       = [Z, K1, K2, K3, D, A, B, C, E, O]

這段code可以驗證一下我們剛剛算的

class Type(type):
    def __repr__(cls):
        return cls.__name__

class O(object, metaclass=Type): pass

class A(O): pass

class B(O): pass

class C(O): pass

class D(O): pass

class E(O): pass

class K1(A, B, C): pass

class K2(D, B, E): pass

class K3(D, A): pass

class Z(K1, K2, K3): pass

print(Z.mro())
# [Z, K1, K2, K3, D, A, B, C, E, O, <class 'object'>]

想知道自己是不是跟python3一樣聰明的話，可以把剛剛上面的例子的Z拿掉K3的繼承，變成Z(K1, K2)，算一遍就知道了(σﾟ∀ﾟ)σ